概率分布

2023-08-14 11:00:00 · bal · 乐小管

概率分布(Probability Distribution)概率分布是指随机变量X小于任何已知实数x的事件可以表示成的函数。用以表述随机变量取值的概率规律。描述不同类型的随机变量有不同的概率分布形式。是概率论的基本概念之一。

概率分布(Probability Distribution)

什么是概率分布

　　概率分布是指随机变量X小于任何已知实数x的事件可以表示成的函数。用以表述随机变量取值的概率规律。描述不同类型的随机变量有不同的概率分布形式。是概率论的基本概念之一。

概率分布的概述

　　离散型随机变量的分布列只取有限个或可列个实数值的随机变量称为离散型随机变量。例如，100件产品中有10件次品，从中随意抽取5件，则其中的次品数X就是一个只取0，1，2，3，4，5的离散型随机变量。描述离散型随机变量的概率分布使用分布列，即给出离散型随机变量的全部取值，及取每个值的概率。例如上面例子中次品数X的分布列为：其中，表示从n个不同事物中取m个的组合数：

　　概率分布第一行写出随机变量X的取值，第二行列出取相应值的概率。这就是X的分布列。常见的离散型随机变量的分布有单点分布、两点分布、正态分布、二项分布、几何分布、负二项分布、超几何分布、泊松分布等。

概率分布的概念

　　概率分布（probabilitydistribution）或简称分布（distribution），是概率论的一个概念。使用时可以有以下两种含义：

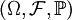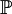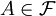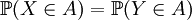　　广义地，概率分布是指称随机变量的概率性质：当我们说概率空间 $(\Omega,\mathcal{F},\mathbb{P})$ 中的两个随机变量X和Y具有同样的分布（或同分布）时，我们是无法用概率 $\mathbb{P}$ 来区别他们的。换言之：称X和Y为同分布的随机变量，当且仅当对任意事件 $A\in\mathcal{F}$ ，有 $\mathbb{P}(X\in A)=\mathbb{P}(Y\in A)$ 成立。

　　但是，不能认为同分布的随机变量是相同的随机变量。事实上即使X与Y同分布，也可以没有任何点ω使得X(ω)=Y(ω)。在这个意义下，可以把随机变量分类，每一类称作一个分布，其中的所有随机变量都同分布。用更简要的语言来说，同分布是一种等价关係，每一个等价类就是一个分布。需注意的是，通常谈到的离散分布、均匀分布、伯努利分布、正态分布、泊松分布等，都是指各种类型的分布，而不能视作一个分布。

　　狭义地，它是指随机变量的概率分布函数。设X是样本空间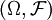 $(\Omega,\mathcal{F})$ 上的随机变量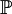， $\mathbb{P}$ 为概率测度，则称如下定义的函数是X的分布函数（distribution function），或称累积分布函数（cumulative distribution function，简称CDF）：

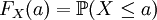　　 $F_X(a)=\mathbb{P}(X\leq a)$ ，对任意实数a定义。

　　具有相同分布函数的随机变量一定是同分布的，因此可以用分布函数来描述一个分布，但更常用的描述手段是概率密度函数（probability density function,pdf）。

分布函数的性质刻划

　　对于特定的随机变量X，其分布函数 $F X$ 是单调不减及右连续，而且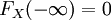 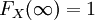$F_X(-\infty)=0$ ， $F_X(\infty)=1$ 。这些性质反过来也描述了所有可能成为分布函数的函数数：

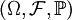　　设 $F[-\infty,\infty]\to[0,1],F(-\infty)=0,F(\infty)=1$ 且单调不减、右连续，则存在概率空间 $(\Omega,\mathcal{F},\mathbb{P})$ 及其上的随机变量X，使得F是X的分布函数，即 $F X = F$

随机变量的分布

　　设P为概率测度,X为随机变量则函数

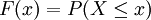　　 $F(x)=P(X\le x)$ ( $x\in\R$ )

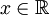　　称为X的概率分布函数.如果将X看成是数轴上的随机点的坐标，那么，分布函数F(x)在x处的函数值就表示X落在区间(-∞,x]上的概率。

　　例如，设随机变量 $X$ 为掷两次骰子所得的点数差，而整个样本空间由36个元素组成，

　　其分布函数是：

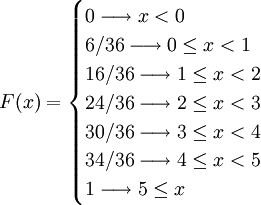
　　 $F(x) = \begin{cases} 0 \longrightarrow x <0 \\6/36 \longrightarrow 0 \le x < 1\\16/36 \longrightarrow 1 \le x < 2\\24/36 \longrightarrow 2 \le x <3\\30/36 \longrightarrow 3 \le x < 4\\34/36 \longrightarrow 4 \le x < 5\\1 \longrightarrow 5 \le x \end{cases}$

离散分布

　　上面所列举的例子都属于离散分布，即分布函数的值域是离散的，比如只取整数值的随机变量就是属于离散分布的。 $F (x)$ 表示随机变量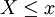 $X\leq x$ 的概率值。如果X的取值只有 $x 1 < x 2 < ... < x n$ ，则：

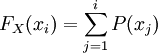
　　 $F_X(x_i)=\sum_{j=1}^iP(x_j)$

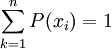
　　 $\sum_{k=1}^nP(x_i)=1$

二项分布

　　二项分布是最重要的离散概率分布之一，由瑞士数学家雅各布·伯努利（Jokab Bernoulli）所发展，一般用二项分布来计算概率的前提是，每次抽出样品后再放回去，并且只能有两种试验结果，比如黑球或红球，正品或次品等。二项分布指出，随机一次试验出现的概率如果为 $p$ ，那么在 $n$ 次试验中出现 $k$ 次的概率为：

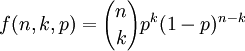
　　 $f(n,k,p)={n\choose k}p^{k}(1-p)^{n-k}$

　　例如，在掷3次骰子中，不出现6点的概率是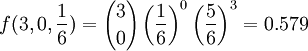： $f(3,0,\frac{1}{6})={3\choose0}\left(\frac{1}{6}\right)^{0}\left(\frac{5}{6}\right)^{3}=0.579$
在连续两次的轮盘游戏中，至少出现一次红色的概率为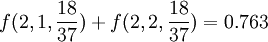： $f(2,1,\frac{18}{37})+f(2,2,\frac{18}{37})=0.763$

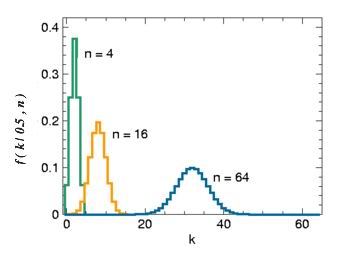
Image:二项分布.jpg

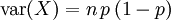
　　二项分布在 $p = 0.5$ 时表现出图像的对称性，而在 $p$ 取其它值时是非对称的。另外二项分布的期望值 $\operatorname{E}(X)=np$ ，以及方差 $\operatorname{var}(X)=n\,p\,(1-p)\!$

正态分布和二项分布

　　在离散分布中如果试验次数 $n$ 值非常大，而且单次试验的概率 $p$ 值又不是很小的情况下，正态分布可以用来近似的代替二项分布。一个粗略的使用正态分布的近似规则是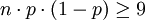： $n\cdot p\cdot(1-p)\geq9$ 。
从二项分布中获得 $μ$ 和 $σ$ 值的方法是

　　期望值 $\mu=n\cdot p$

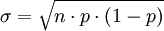
　　标准差 $\sigma=\sqrt{n\cdot p\cdot(1-p)}$

　　如果 $σ > 3$ ，则必须采用下面的近似修正方法：

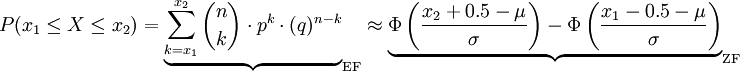
　　 $P(x_1\leq X\leq x_2)=�brace{\sum_{k=x_1}^{x_2}{n\choose k}\cdot p^k\cdot(q)^{n-k}}_{\mathrm{EF}}\approx�brace{\Phi\left(\frac{x_2+0.5-\mu}{\sigma}\right)-\Phi\left(\frac{x_1-0.5-\mu}{\sigma}\right)}_{\mathrm{ZF}}$

　　注： $q = 1 - p$ ,EF：二项分布，ZF：正态分布)

　　上（下）临界值分别增加（减少）修正值0.5的目的是在 $σ$ 值很大时获得更精确的近似值，只有 $σ$ 很小时，修正值0.5可以不被考虑。

　　例如，随机试验为连续64次掷硬币，获得的国徽数位于32和42之间的概率是多少？用正态分布计算如下，

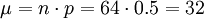
　　 $\mu=n\cdot p=64\cdot0.5=32$

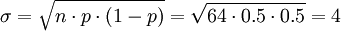
　　 $\sigma=\sqrt{n\cdot p\cdot(1-p)}=\sqrt{64\cdot0.5\cdot0.5}=4$

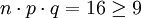　　 $n\cdot p\cdot q=16\geq9$ ，符合近似规则，应用 $z$ -变换：

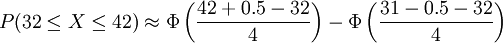
　　 $P(32\leq X\leq42)\approx\Phi\left(\frac{42+0.5-32}{4}\right)-\Phi\left(\frac{31-0.5-32}{4}\right)$

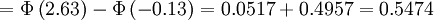
　　 $=\Phi\left(2.63\right)-\Phi\left(-0.13\right)=0.0517+0.4957=0.5474$

Image:标准正态分布.jpg

　　在运用z表格时注意到利用密度函数的对称性来求出z为负值时的区域面积。

超几何分布

　　作为离散概率分布的超几何分布尤其指在抽样试验时抽出的样品不再放回去的分布情况。在一个容器中一共有 $N$ 个球，其中 $M$ 个黑球， $(N - M)$ 个红球，通过下面的超几何分布公式可以计算出，从容器中抽出的 $n$ 个球中（抽出的球不放回去）有 $k$ 个黑球的概率是多少：

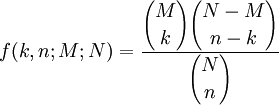
　　 $f(k,n;M;N)=\frac{\displaystyle{M\choose k}{N-M\choose n-k}}{\displaystyle{N\choose n}}$

　　例如，容器中一共10个球，其中6个黑色，4个白色，一共抽5次（抽出的球不放回去），在这5个球中有3个黑球的概率是：

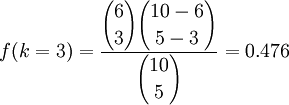
　　 $f(k=3)=\frac{\displaystyle{6\choose3}{10-6\choose5-3}}{\displaystyle{10\choose5}}=0.476$

超几何分布和二项分布的关系

　　和二项分布不同的是，在超几何分布中，特别强调的是抽出的样品在下一次抽取前不再放回去，但是如果抽取的次数 $n$ 和总共样品数 $N$ 相比很小(大约 $n / N < 0,05$ )，这时在计算上二项分布和超几何分布相互间则没有主要的区别，此时人们更愿意采用二项分布的方法，因为在数学计算上二项分布要简单一些。

泊松近似

　　泊松近似是二项分布的一种极限形式。其强调如下的试验前提：一次抽样的概率值 $p$ 相对很小，而抽取次数 $n$ 值又相对很大。因此泊松分布又被称之为罕有事件分布。泊松分布指出，如果随机一次试验出现的概率为 $p$ ，那么在 $n$ 次试验中出现 $k$ 次的概率按照泊松分布应该为：

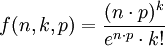
　　 $f(n,k,p)=\frac{(n\cdot p)^k}{e^{n\cdot p}\cdot k!}$

　　其中数学常数 $e = 2.71828...$ (自然对数的底数)
例如，某工厂在生产零件时，每200个成品中会有1个次品，那么在100个零件中最多出现2个次品的概率按照泊松分布应该是：

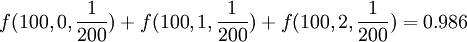
　　 $f(100,0,\frac{1}{200})+f(100,1,\frac{1}{200})+f(100,2,\frac{1}{200})=0.986$

　　在实践中如果遇到 $n$ 值很大导致二项分布难于计算时，可以考虑使用泊松分布，但前提是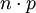 $n\cdot p$ 必须趋于一个有限极限。采用泊松分布的一个不太严格的规则是：

　　 $n\ge100$

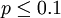
　　 $p\le0.1$

连续分布

　　设 $X$ 是具有分布函数 $F$ 的连续随机变量，且F的一阶导数处处存在，则其导函数

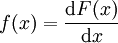
　　 $f(x)=\frac{\operatorname{d}F(x)}{\operatorname{d}x}$

　　称为 $X$ 的机率密度函数。
每个机率密度函数都有如下性质：

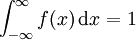
　　 $\int_{-\infty}^\infty f(x)\,{\rm d}x=1$

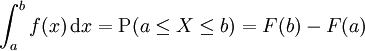
　　 $\int_a^bf(x)\,{\rm d}x=\operatorname{P}(a\le X\le b)=F(b)-F(a)$

　　第一个性质表明，机率密度函数与 $x$ 轴形成的区域的面积等于1，第二个性质表明，连续随机变量在区间[ab]的概率值等于密度函数在区间[ab]上的积分，也即是与 $X$ 轴在[ab]内形成的区域的面积。因为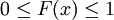 $0\le F(x)\le1$ ，且 $f (x)$ 是 $F x)$ 的导数，因此按照积分原理不难推出上面两个公式。

　　正态分布和指数分布 $t$ -分布， $F$ -分布以及 $ξ 2$ -分布都是连续分布。

正态分布

　　连续随机变量的机率密度函数如果是如下形式，

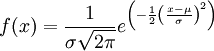
　　 $f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^\left(-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2\right)$

　　那么这个连续分布被称之为正态分布，或者高斯分布。其密度函数的曲线呈对称钟形，因此又被称之为钟形曲线，其中 $μ$ 是平均值， $σ$ 是标准差。正态分布是一种理想分布，许多典型的分布，比如成年人的身高，汽车轮胎的运转状态，人类的智商值（IQ），都属于或者说至少接近正态分布。同样按照连续分布的定义，正态机率密度函数具有和普通机率密度函数类似的性质：

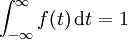
　　 $\int_{-\infty}^\infty f(t)\,{\rm d}t=1$

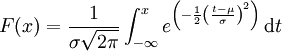
　　 $F(x)=\frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^xe^\left(-\frac{1}{2}\left(\frac{t-\mu}{\sigma}\right)^2\right)\,{\rm d}t$

　　如果给出一个正态分布的平均值 $μ$ 以及标准差 $σ$ ，可以根据上面的第二个公式计算出任一区间的概率分布情况。但是如上的计算量是相当庞大的，没有计算机的辅助基本是不可能的，解决这一问题的方法是借助 $z$ -变换以及标准正态分布表格( $z$ -表格)。

　　中间值 $μ = 0$ 以及标准差 $σ = 1$ 的正态分布被称之为标准正态分布，其累积分布函数是

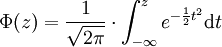
　　 $\Phi(z)=\frac1{\sqrt{2\pi}}\cdot\int_{-\infty}^ze^{-\frac12t^2}\mathrm{d}t$

　　将普通形式的正态分布变换到标准正态分布的方法是

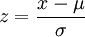
　　 $z=\frac{x-\mu}{\sigma}$

　　例如，已知一正态分布的 $μ = 5$ ， $σ = 3$ ，求区间概率值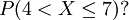 $P(4<X\le7)?$ 计算过程如下，

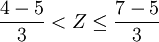
　　 $\frac{4-5}{3}<Z\le\frac{7-5}{3}$

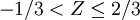
　　 $-1/3<Z\le2/3$

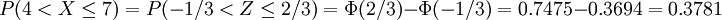
　　 $P(4<X\le7)=P(-1/3<Z\le2/3)=\Phi(2/3)-\Phi(-1/3)=0.7475-0.3694=0.3781$

　　其中 $Φ(z)$ 值通过查 $z$ -表格获得。

_{免责声明：本内容来源于第三方作者授权、网友推荐或互联网整理，旨在为广大用户提供学习与参考之用。所有文本和图片版权归原创网站或作者本人所有，其观点并不代表本站立场。如有任何版权侵犯或转载不当之情况，请您通过400-62-96871或关注我们的公众号与我们取得联系，我们将尽快进行相关处理与修改。感谢您的理解与支持！}

名词术语

统计术语

综合条目

阅读全文