Z检验
Z检验(Z Test)
什么是Z检验
Z检验是一般用于大样本(即样本容量大于30)平均值差异性检验的方法。它是用标准正态分布的理论来推断差异发生的概率,从而比较两个平均数的差异是否显著。
当已知标准差时,验证一组数的均值是否与某一期望值相等时,用Z检验。
另外,对于Z检验我国的统计学教材大多采用U检验的说法。而国外英文统计学书籍,大多采用Z检验。
Z检验的步骤[1]
统计检验的基本原理
统计检验是先对总体的分布规律作出某种假说,然后根据样本提供的数据,通过统计运算,根据运算结果,对假说作出肯定或否定的决策。如果现要检验实验组和对照组的平均数(μ1和μ2)有没有差异,其步骤为:
1.建立虚无假设,即先认为两者没有差异,用 H0:μ1 = μ2 表示;
2.通过统计运算,确定假设 H0 成立的概率 P。
3. 根据 P 的大小,判断假设 H0 是否成立。如下表所示。
Z检验法适用于大样本(样本容量大于30)的两平均数之间差异显著性检验的方法。它是通过计算两个平均数之间差的Z分数来与规定的理论Z值相比较,看是否大于规定的理论Z值,从而判定两平均数的差异是否显著的一种差异显著性检验方法。其一般步骤:
第一步:建立虚无假设 H0:μ1 = μ2 ,即先假定两个平均数之间没有显著差异,
第二步:计算统计量Z值,对于不同类型的问题选用不同的统计量计算方法,
1、如果检验一个样本平均数(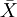 )与一个已知的总体平均数(μ0)的差异是否显著。其Z值计算公式为:
)与一个已知的总体平均数(μ0)的差异是否显著。其Z值计算公式为:
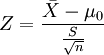
其中:
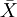 是检验样本的平均数;
是检验样本的平均数;
- μ0是已知总体的平均数;
- S是样本的标准差;
- n是样本容量。
2、如果检验来自两个的两组样本平均数的差异性,从而判断它们各自代表的总体的差异是否显著。其Z值计算公式为:
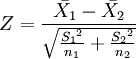
其中:
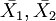 是样本1,样本2的平均数;
是样本1,样本2的平均数;
- S1,S2是样本1,样本2的标准差;
- n1,n2是样本1,样本2的容量。
第三步:比较计算所得Z值与理论Z值,推断发生的概率,依据Z值与差异显著性关系表作出判断。如下表所示:
第四步:根据是以上分析,结合具体情况,作出结论。
Z检验举例[1]
某项教育技术实验,对实验组和控制组的前测和后测的数据分别如下表所示,比较两组前测和后测是否存在差异。
由于n>30,属于大样本,所以采用Z检验。由于这是检验来自两个不同总体的两个样本平均数,看它们各自代表的总体的差异是否显著,所以采用双总体的Z检验方法。
计算前测Z的值:
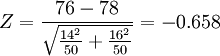
- ∵|Z|=0.658<1.96
- ∴ 前测两组差异不显著。
再计算后测Z的值:
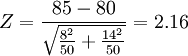
- ∵|Z|= 2.16>1.96
- ∴ 后测两组差异显著。
参考文献
免责声明:本内容来源于第三方作者授权、网友推荐或互联网整理,旨在为广大用户提供学习与参考之用。所有文本和图片版权归原创网站或作者本人所有,其观点并不代表本站立场。如有任何版权侵犯或转载不当之情况,请您通过400-62-96871或关注我们的公众号与我们取得联系,我们将尽快进行相关处理与修改。感谢您的理解与支持!




















请先 登录后发表评论 ~